For the Algorithmic Emergence Assignment, we were asked to propose an architectural installation as part of the Mies van der Rohe pavilion under the scope of recursive systems. In other words, how would nature take over a contained space. As a case study, I chose to observe the growth system of Corals.
BRIEF & KEY CONCEPTS
// Coral Reef Extinction
Due to the exploitation of natural resources the past few decades, the earth’s resources have depleted faster than anticipated. Primary ecosystem are being shaken down by the global warming causing repercussions on all living creatures. For example Coral Reefs are going extinct. It is said that:
– 90% of Coral reefs will become extinct by 2050
– They occupy less than 1% of the ocean floor yet they are home to more than 25% of marine biodiversity.
The design intention is to understand & replicate the growth system of the Coral reefs as we were asked to work on recursive patterns. During the investigation process, I identified the branching growth & the scaled repetition as the most unconventional & unusual pattern. The intervention will try to merge both these growth method employed by the coral to reproduce.
Barcelona Pavilion

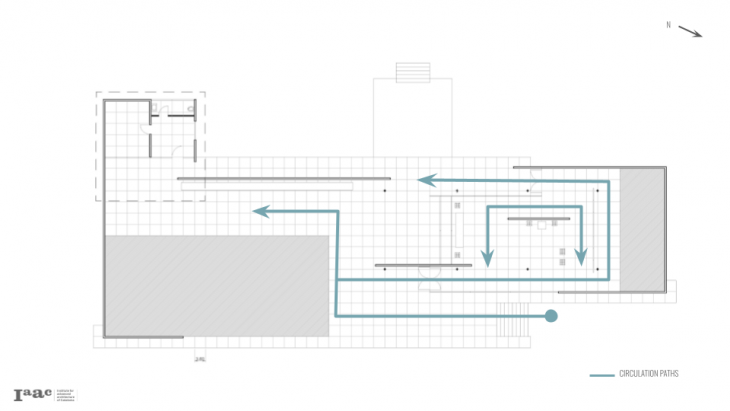
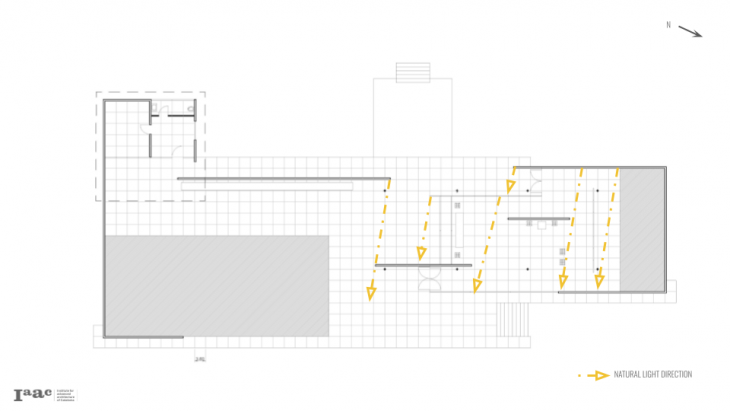
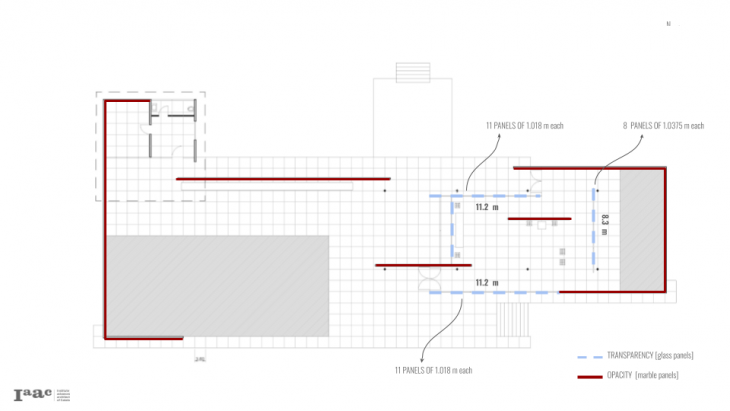
BASE GEOMETRY
1- Use of ICOSAHEDRON as a Base Geometry which changes in scale
2- Use of Voronoi to create paths for growth of icosahedron
PSEUDO-CODE
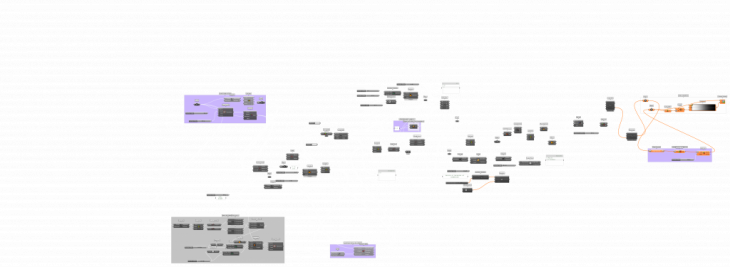
DETAILED STEPS
- Glass panel Setup [11.2 x 3.28 m]
- Create 11 Divisions
- Add division for mullions
- Define one portion as a base plane for growth
- Populate plane with points
- Divide plane using Voronoi Pattern
- Intersection of Voronoi & Rectangle boundary
- Select random points along curve
- Define inner growth perimeter
- Populate inner perimeter
- Create lines connecting points from outer & inner perimeter
- Create Voronoi path for shortest link between outer & inner
- Points along Voronoi curve
- Icosahedron along points of curve, varying in scale

