Lorenz Attractor – Particle System | Processing
A particle system is a technique in game physics, motion graphics, and computer graphics that uses a large number of very small sprites, 3D models, or other graphic objects to simulate certain kinds of “fuzzy” phenomena, which are otherwise very hard to reproduce with conventional rendering techniques – usually highly chaotic systems, natural phenomena, or processes caused by chemical reactions.
Attractors In the mathematical field of dynamical systems, an attractor is a set of numerical values toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.
In finite-dimensional systems, the evolving variable may be represented algebraically as an n-dimensional vector. The attractor is a region in n-dimensional space. In physical systems, the n dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate.
If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a point, a finite set of points, a curve, a manifold, or even a complicated set with a fractal structure known as a strange attractor (see strange attractor below). If the variable is a scalar, the attractor is a subset of the real number line. Describing the attractors of chaotic dynamical systems has been one of the achievements of chaos theory.
A trajectory of the dynamical system in the attractor does not have to satisfy any special constraints except for remaining on the attractor, forward in time. The trajectory may be periodic or chaotic. If a set of points is periodic or chaotic, but the flow in the neighborhood is away from the set, the set is not an attractor, but instead is called a repeller.
Lorenz System The Lorenz system is a system of ordinary differential equations (the Lorenz equations, note it is not Lorentz) first studied by Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly.
Lorenz Attractors The Lorenz attractor is an attractor that arises in a simplified system of equations describing the two-dimensional flow of fluid of uniform depth , with an imposed temperature difference , under gravity , with buoyancy , thermal diffusivity , and kinematic viscosity .
This project aim to practice how to write the code using processing to simulate the movement of particles in specific direction that given by mathematical formula.
The code have been developed by using the PVector object in processing in order to create the particles system to perform visually with the Lorenz Attractor rule. Basically, the rule is using math formula with the constant through frame rate of the processing sketch.


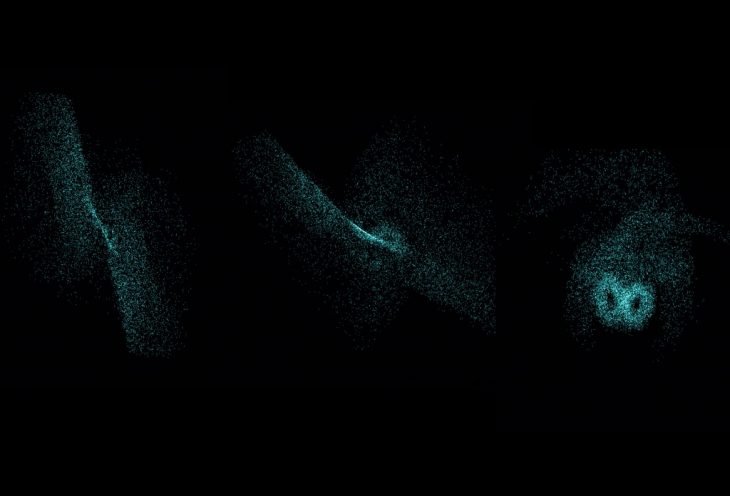
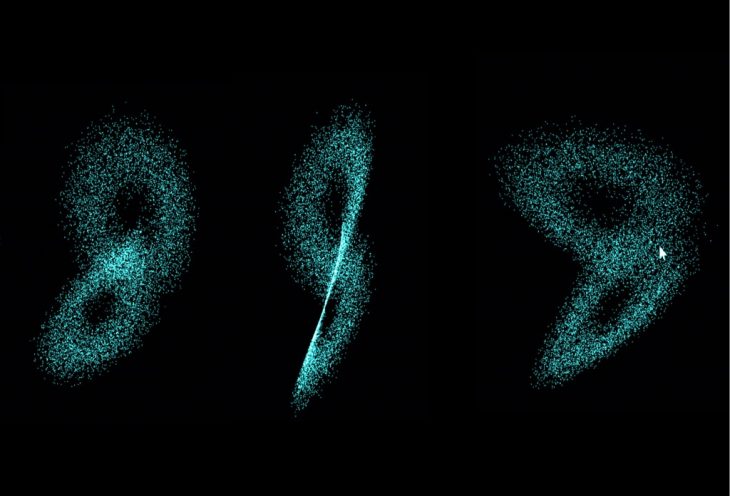

</p>
Lorenz Attractor is a project of IaaC, Institute for Advanced Architecture of Catalonia developed at Master of Advanced Architecture in 2016/17 by:
Student: Nisarg sheth
Faculty: Angelos Chronis