Introduction
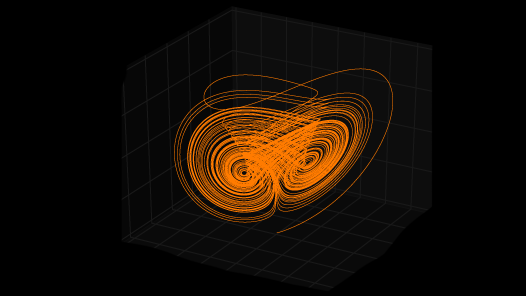
Edward Lorenz’s first weather model exhibited chaotic behavior, but it involved a set of 12 nonlinear differential equations. Lorenz decided to look for complex behavior in an even simpler set of equations, and was led to the phenomenon of rolling fluid convection. The exercise, being set in a premise of “nature taking over architecture”, this is an experiment in visualizing nonlinear differential equations for their architectural capacities. The Chua Attractor is one of the chaotic attractors based on 3 nonlinear differential equations which are controlled by 6 parameters.

// chua attractor
The chua attractor is governed by the equations as indicated above. These equations can be controlled by a linear equation viz. G(x), and five constant parameters, viz. ?, ?, ?, ?, ? .
.equations derivatives
- dx/dt = ?(y-x-G(x))
- dy/dt = ?(x-y+z)
- dz/dt = -?y
.equation parameters
- G(x) = ? x + (?+?) (abs (x+1) – abs (x-1) )
- t = time
.equation variables
?, ?, ?, ?, ?
//variations
The topologies obtained from the curves resulting from the chua attractor equations can be controlled with the help of equation parameters, viz. ?, ?, ?, ?, ?.
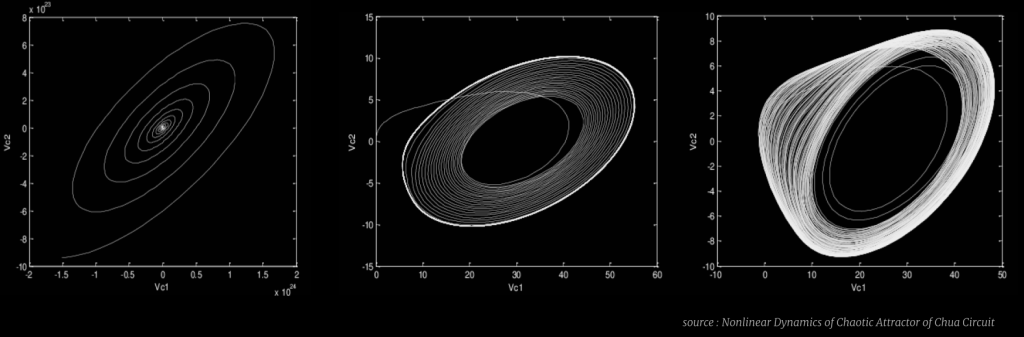
.single scroll attractors
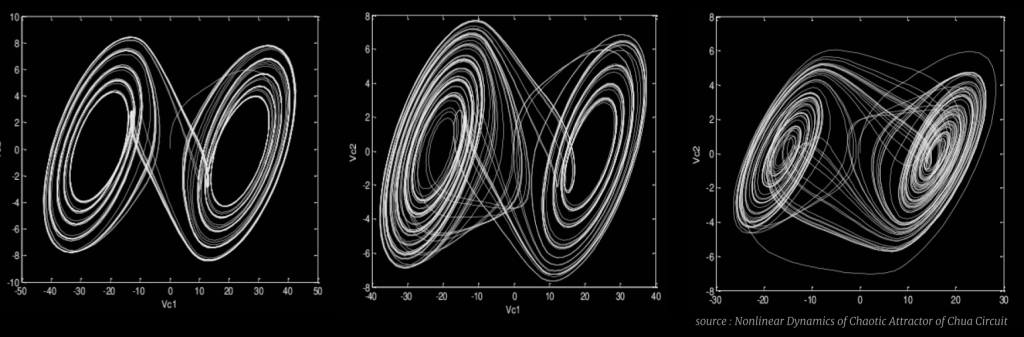
.multi scroll attractors
//pseudo code
Anemone is used to run the delta operations individually on x, y and z coordinates. Constants ?, ?, ?, ?, ? help control the topology of the resultant non-linear, non-periodic curve.
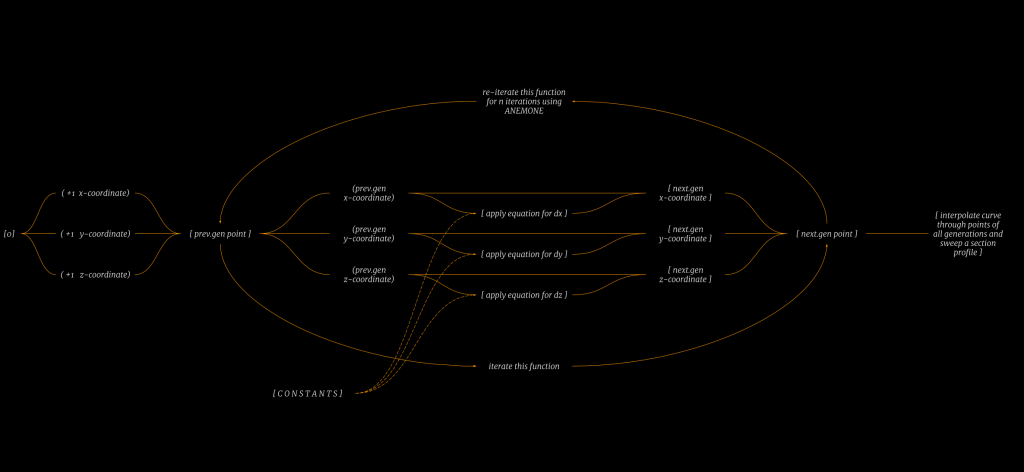
//grasshopper definition
Following is the grasshopper definition that was developed based on the pseudo code above.
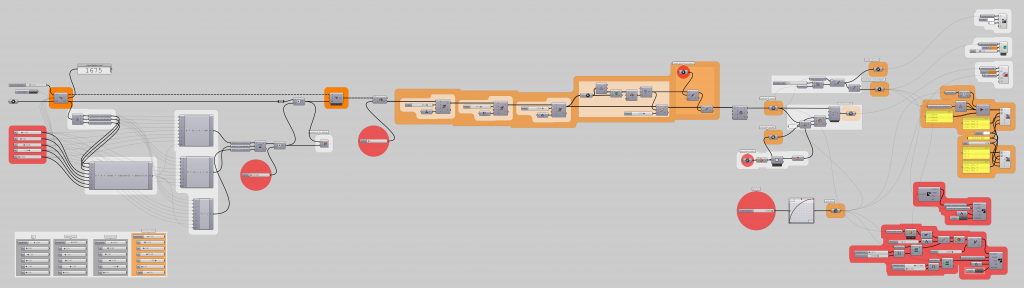
//iterations
The chua attractor is governed by the equations as indicated above. These equations are controlled by a linear equation viz. G(x), and five constant parameters, viz. ?, ?, ?, ?, ? .
.iteration 01
The parameters indicated above result in a loosely woven single scroll chaotic attractor.
.equations derivatives
- dx/dt = ?(y-x-G(x))
- dy/dt = ?(x-y+z)
- dz/dt = -?y
.equation parameters
- G(x) = ? x + (?+?) (abs (x+1) – abs (x-1) )
- t = time
.equation variables
? = 1.000 | ? = 1.000 | ? = 1.000 | ? = -3.000 | ? = 0.000
t = 0.010
i = 3000 iterations
.iteration 02
The parameters indicated above result in a tightly woven single scroll chaotic attractor.
.equations derivatives
- dx/dt = ?(y-x-G(x))
- dy/dt = ?(x-y+z)
- dz/dt = -?y
.equation parameters
- G(x) = ? x + (?+?) (abs (x+1) – abs (x-1) )
- t = time
.equation variables
? = 5.000 | ? = 1.000 | ? = 10.000 | ? = -2.000 | ? = 0.000
t = 0.010
i = 3000 iterations
.iteration 03
The parameters indicated above result in a tightly woven multi scroll chaotic attractor.
.equations derivatives
- dx/dt = ?(y-x-G(x))
- dy/dt = ?(x-y+z)
- dz/dt = -?y
.equation parameters
- G(x) = ? x + (?+?) (abs (x+1) – abs (x-1) )
- t = time
.equation variables
? = 20.000 | ? = 1.000 | ? = 30.000 | ? = -1.000 | ? = 0.000
t = 0.010
i = 3000 iterations
.iteration final
The chua attractor is governed by the equations as indicated above. These equations are controlled by a linear equation viz. G(x), and five constant parameters, viz. ?, ?, ?, ?, ? . The parameters indicated above result in a tightly woven multi scroll chaotic attractor.
.equations derivatives
- dx/dt = ?(y-x-G(x))
- dy/dt = ?(x-y+z)
- dz/dt = -?y
.equation parameters
- G(x) = ? x + (?+?) (abs (x+1) – abs (x-1) )
- t = time
.equation variables
? = 14.500 | ? = 1.000 | ? = 25.580 | ? = -1.000 | ? = 0.000
t = 0.010
i = 1475 iterations
//architectural intervention



//summary video