The project explores topological optimization and material distribution on freeform meshes using Galapagos and Millipede. The aim is to produce any type of freeform mesh and through evolutionary solvers achieve the optimum material distribution which will result in the use of the least possible material to achieve the surface.
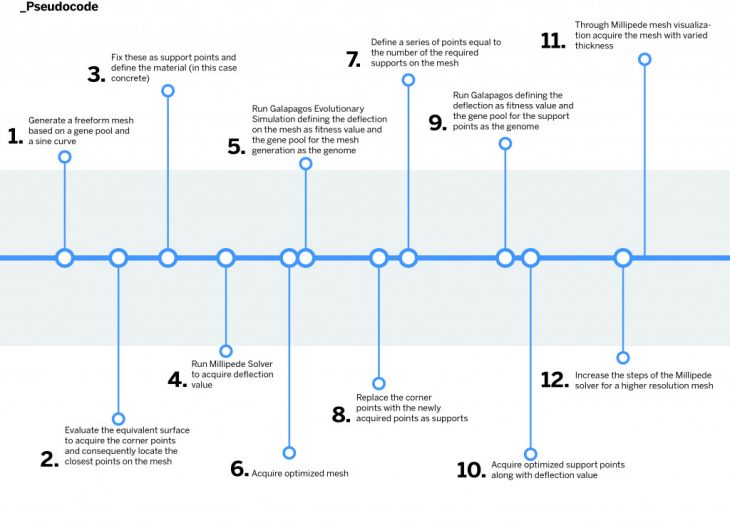
- The pseudocode above describes the process which can be broken down into steps:
- Generate a freeform mesh based on a gene pool and sine curve
- Evaluate the equivalent surface to acquire the corner points and consequently locate the closest points on the mesh
- Fix these as support points and define the material (in this case concrete)
- Run Millipede Solver to acquire deflection value
- Run Galapagos Evolutionary Simulation defining the deflection on the mesh as fitness value and the gene pool for the mesh generation as the genome
- Acquire optimized mesh
- Define a series of points equal to the number of the required supports on the mesh
- Replace the corner points with the newly acquired points as supports
- Run Galapagos defining the deflection as fitness value and the gene pool for the support points as the genome
- Acquire optimized support points along with deflection value
- Through Millipede mesh visualization acquire the mesh with varied thickness
- Increase the steps of the Millipede solver for a higher resolution mesh
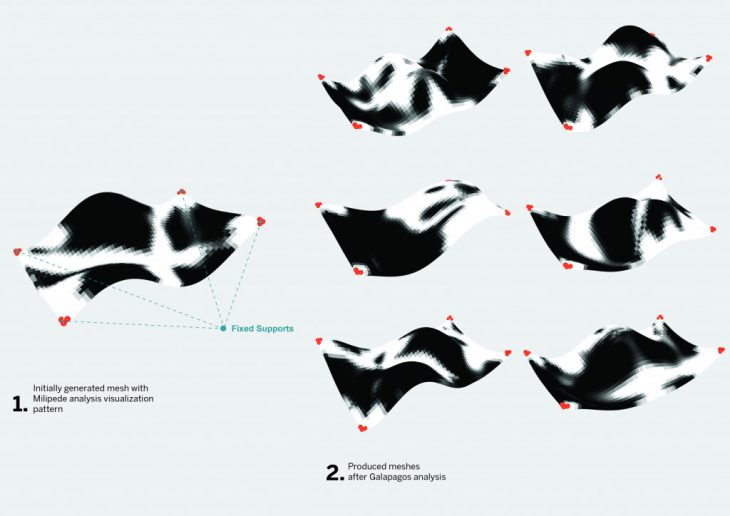
Production of mesh using corner points as anchors or support points and the iterations produced by Galapagos.


Catalogues of produced iterations
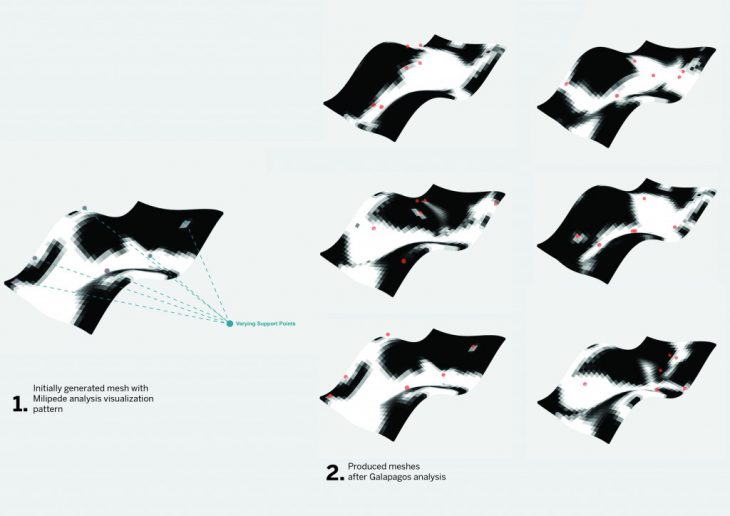
Optimized mesh using random points as anchors or support points and the iterations produced by Galapagos.



Catalogues of produced iterations

</p>
3D View of optimized mesh with visualized thickness information.