What are the morphological possibilities a simple sphere holds?

This excercise explores some of these different possibilities through algorithmic manipulations. These were based on euclidean transformations and data list manipulations using the visual programming interface Grasshopper 3D. The approach for creating Spiraling tentacles was to first divise an initial logic based on a sphere’s geometry and then implement a new and different geometry that would respond to these initially generated parameters.

Process

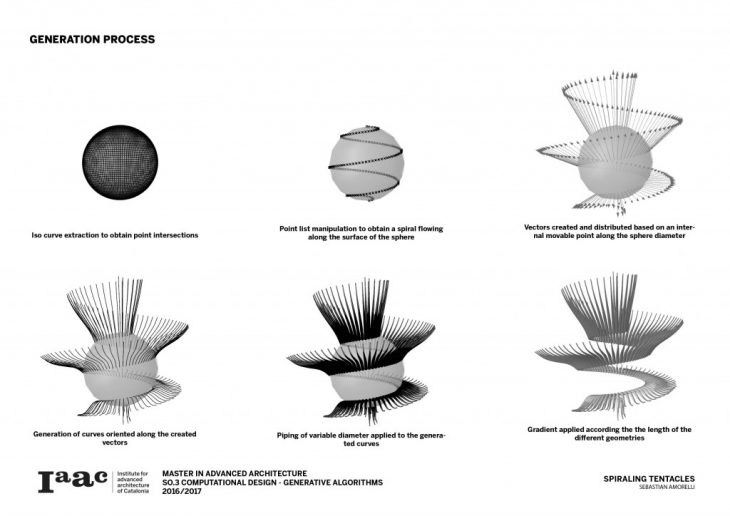
By extracting the sphere’s horizontal Isocurves, dividing them and then manipulating the resulting list of points a spherical path is created along the surface of the geomtery. Then by defining a mobile attractor point which moves along an internal vertical diameter, different vectors are generated along the spiral. These change their orientation and magnitude based on their proximity to the internal point. Finally the “tentacles” are created by defining a set of curves along these vectors and then creating a pipe of variable radiuses, this way creating a new geometry along the sphere. The final colour of each “tentacle” responds to its final length.

Variations

By manipulating the initial parameters derived from the sphere, multiple shapes with diverse configurations start to arise.

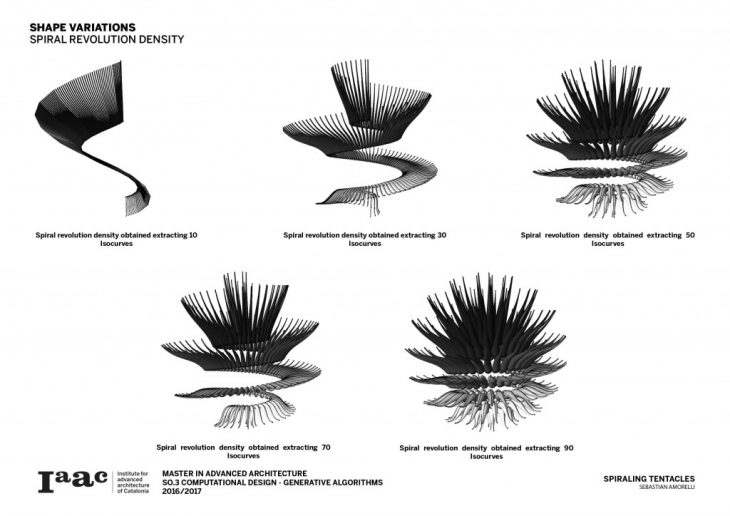
The amount of Isocurves extracted from the sphere determines the density and number of turns of the spiral created along its surface.

The number of times each Isocurve is divided determines the tentacle population along the spiral.

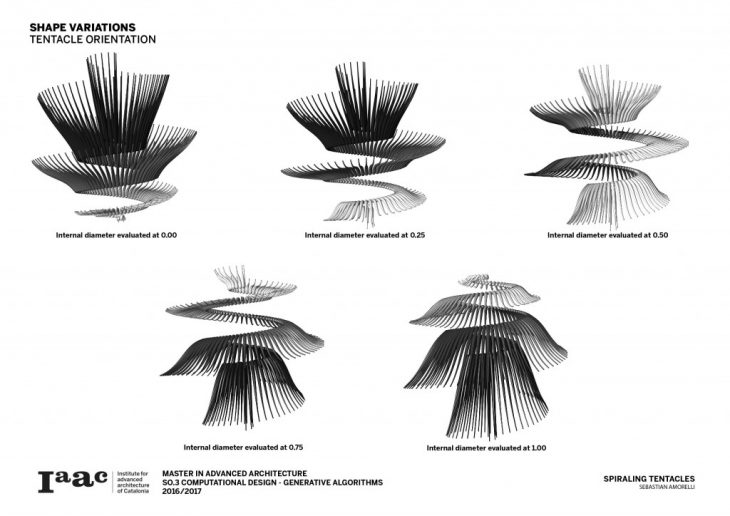
Finally by manipulating the position of the internal point along the diameter, the size and orientation of the tentacles can be changed.

MASTER IN ADVANCED ARCHITECTURE
SO.03 COMPUTATIONAL DESIGN – GENERATIVE ALGORITHMS
2016/2017
TUTORS: RODRIGO AGUIRRE, ALDO SOLLAZO
STUDENT: SEBASTIAN AMORELLI