Triangulated Attraction

The objective of this exercise is to apply computational design strategies as a form finding tool. The exercise is focused on a threedimensional manipulation of a simple sphere performed by combining multiple transformations.
In this case the transformation is from a single sphere to a triangulated population of spheres surrounded by disks.

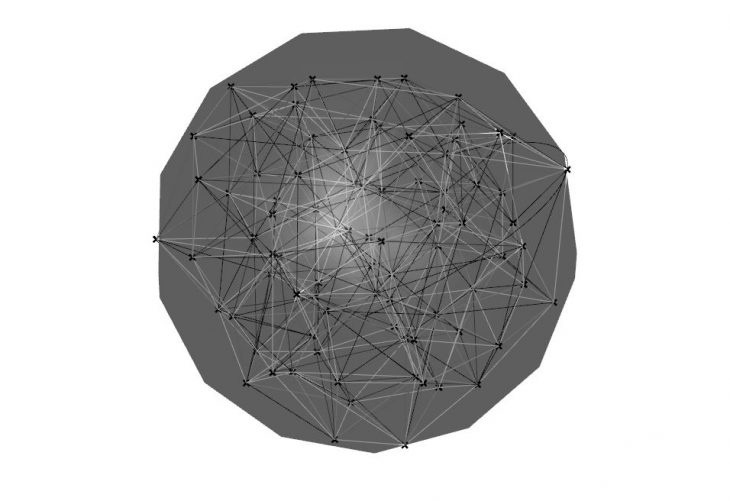
A triangulated population of points inside a sphere.

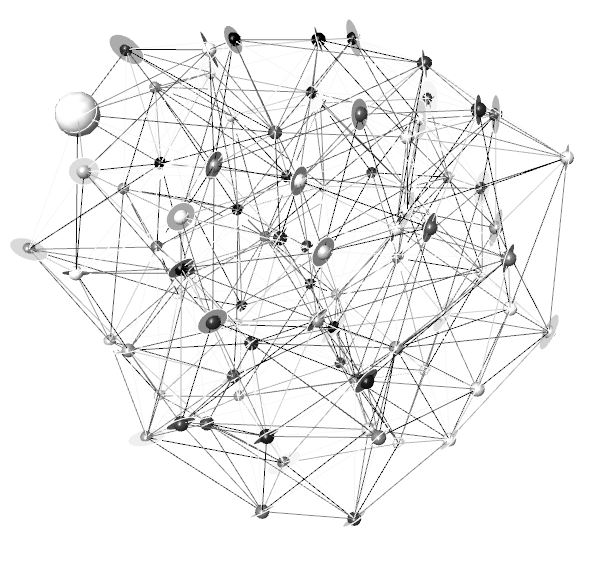
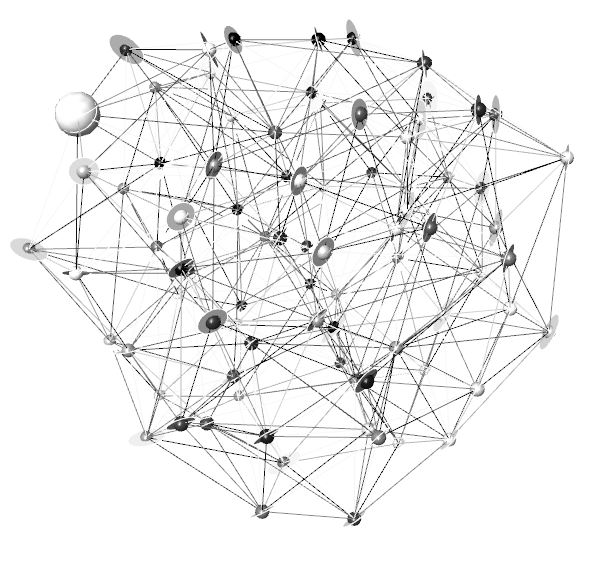
By replacing the points with spheres and disks it was possible to create a system of lines and solids that are interconnected in a network-like way.

A network of solids and lines.

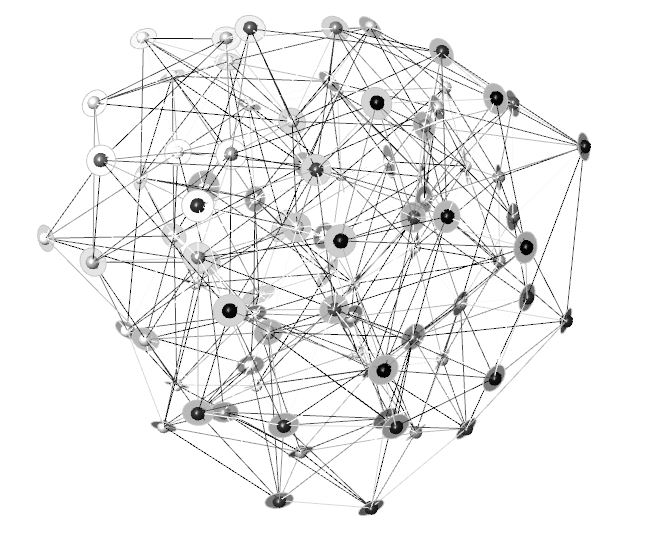
Moreover, an attractor Solid was created inside the network which could only move on a certain path. While moving the attractor the disks that are populating the network, always have to orient their normals-faces towards the attractor. With this new relationship between attractor and surfaces it was possible to visualise an attraction that takes place in a triangulated network.

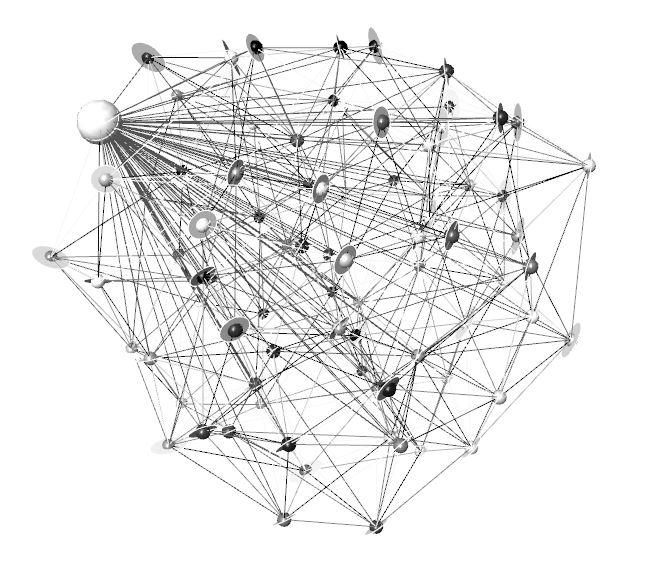
The disks always orient their normals-faces towards the attractor solid.

By moving the attractor inside the population of solids and surfaces and by applying a gradient colour that relates to the distance between the individuals and the attractor, we were able to see the change in patterns that occur. Thus, a catalogue of patterns was created:

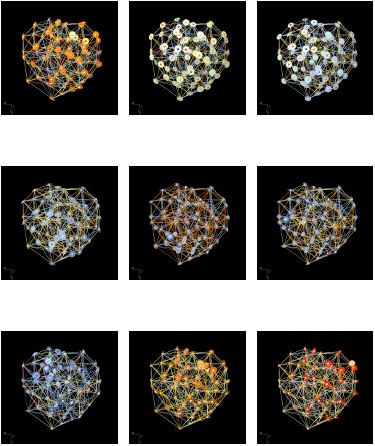
Catalogue of movement with triangulation

Catalogue of movement without triangulation.

Catalogue of movement with the distance lines enabled.

The following video shows the triangulated attractive system in motion:

Triangulated Attraction is a project of IaaC, Institute for Advanced Architecture of Catalonia
developed at Master in City & Technology in 2016/2017 by:
Students: Alex Mademo
Faculty: Rodriguo Aguirre, Aldo Sollazo